Bayesian Network Representation of Joint Normal Distributions - Cascading Regressions Model

This post is the first of a series discussing the Bayesian Network representation of multivariate normal distributions. A joint normal distribution being fully specified by its mean vector and its covariance matrix is not simple to interact with as its Bayesian network equivalent. Representing a joint normal distribution as a Bayesian network enables visualizing and interacting with the distribution through the lens of probabilistic graphical models with TKRISK®.

We demonstrate in this post a simple yet powerful approach using a cascading regressions approach.

A normal distribution $\mathcal{N}(m, v)$ is fully specified using two parameters: its mean $m\in\mathbb R$ and its variance $v\in\mathbb R_+$. Likewise, a $n$-dimensional multivariate normal distribution $\mathcal{N}(M, V)$ is fully specified by its mean vector $M\in\mathbb R^n$ and covariance matrix $V\in\mathbb R^n\times \mathbb R^n$.

The latter can also be represented as a Bayesian Network, more specifically as a Gaussian Bayesian network [KF09] [CBLV20].

In what follows we will be working with a vector of random variables $X=(X_1,..., X_n)$ following a multivariate normal distribution $\mathcal{N}(M, V)$.

By definition $M = (\mathbb E[X_i])_{i \in \llbracket 1, n\rrbracket}$ and $V = (cov(X_i, X_j))_{(i,j) \in \llbracket 1, n\rrbracket^2}$.

Through basic matrix operations we will show how $\mathcal{N}(M, V)$ can be represented through a cascading regression model which is a particular case of a linear Gaussian Structural Equation Model (SEM) [DFS11][PK19], the latter having a direct Gaussian Bayesian Network equivalent.

Applying LDL decomposition on $V$ yields $V = L D L^T$ with $L$ being unit lower triangular and $D$ diagonal.

Therefore:$$X - M\sim L E$$ with $E\sim \mathcal{N}(0, D)$.

Introducing $B \triangleq I - L^{-1}$ with $I$ being the n-dimensional identity matrix, we obtain the structural model:$$X \sim (I-B)M + BX + E$$The above specifies a Gaussian Bayesian Network which can be expressed explicitly for each variable:$$\forall i \in \llbracket 1, n\rrbracket, X_i \sim \tilde{m}_i + \sum_{j=1}^{i-1} b_{i,j}X_j + e_i$$with:

• $\tilde{m}_i=m_i - \sum_{j=1}^{i-1} b_{i,j}m_j$
• $E = (e_i)_{1\leq i \leq n}$
• $B = \begin{bmatrix}1 & 0 & \cdots & 0 \\b_{2,1} & \ddots & \ddots & \vdots \\\vdots & \ddots & \ddots & 0\\b_{n,1} & \cdots & b_{n,n-1} & 1\\\end{bmatrix}$

The terms of matrix B can be interpreted as the linear regression coefficients of each variable $X_i$ over its parents $Pa(X_i) = \{X_1, ..., X_{i-1}\}$.

It is important to note that a different order in the variables will lead to a different Bayesian Network structure, representing however the exact same joint distribution.

The above approach is simple, computationally efficient and allows Bayesian Networks generation straight from any dataset for which variables are assumed normally distributed. Working with LDL decomposition and requiring only unit lower triangular matrix inversion means the algorithm is flexible to handle any case of covariance matrix (even non definite) and thus any multivariate normal distribution.

It is common to work on standardized normal distributions, i.e. with zero mean and unit variance:

• $M=0$
• $\textit{Diag}(V) = [1, \cdots, 1]$

In this case covariance and correlation matrices are one and the same. This is a convenient setup which does not imply loss of generality as non-normalized marginals can be recovered by shifting and scaling the normalized ones. Working on normalized space allows for direct comparison of dependencies between variables as these are independent of their actual magnitude.

For a self-contained graph representation, contrary to the above generic approach, the Gaussian Bayesian Network is insufficient and would require additional deterministic nodes to apply shifting and scaling (shifting and scaling directly a node on the Bayesian Network would propagate on its children and thus alter the joint distribution).

For sake of simplicity we will present examples on standardized normal distributions only.

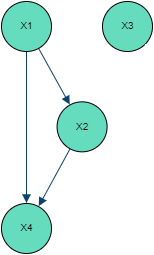
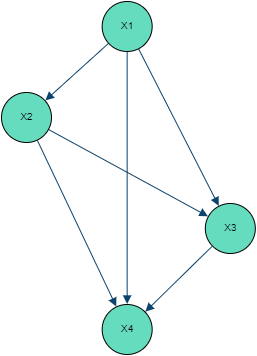
To visualize and interpret the above approach, we will take basic examples of 4 dimensional multivariate normal distributions.

$V = \begin{bmatrix}1 & 0 & 0 & 0 \\0 & 1 & 0 & 0 \\0 & 0 & 1 & 0\\0 & 0 & 0 & 1\\\end{bmatrix}$ $\implies$

$V = \begin{bmatrix}1 & 0.1 & 0 & 0 \\0.1 & 1 & 0 & 0.5 \\0 & 0 & 1 & 0\\0 & 0.5 & 0 & 1\\\end{bmatrix}$ $\implies$

$V = \begin{bmatrix}1 & 0.1 & 0.2 & 0.3 \\0.1 & 1 & 0.4 & 0.5 \\0.2 & 0.4 & 1 & 0.6\\0.3 & 0.5 & 0.6 & 1\\\end{bmatrix}$ $\implies$